NP (CSCI-570)

NP and Computational Intractability

Definition

• If Problem X is at least as hard as Problem Y, it means that if we could solve X, we could also solve Y.
• $Y\le _{p}X$
  • Y is polynomial-time reducible to X
  • Y can be solved using a polynomial number of computational steps plus a polynomial number of calls to a blackbox that solves X
  • X is at least as hard as Y

Some NP Problems

Independent Set

Given a graph $G=(V, E)$, we say a set of nodes $S\subseteq V$ is independent if no two nodes in S are joined by an edge.
Optimization Version: find the maximum size of an independent set.
Decision Version: whether G has an independent set of size at least a given k.

Vertex Cover

Given a graph $G=(V, E)$, we say that a set of nodes $S\subseteq V$ is a vertex cover if every edge in E has at least one end in S.

Let $G=(V, E)$, then $S$ is a independent set if and only if its complement $V-S$ is a vertex cover set.
Independent Set $\le _{p}$ Vertex Cover.
Vertex Cover $\le _{p}$ Independent Set.
Vertex Cover Problem and Independent Set Problem are in the same complexity class.

Let $G = (V , E)$ be a graph. Then S is an independent set if and only if its complement V − S is a vertex cover.

Set Cover

Given a set $U$ of $n$ elements, a collection $S_1$, . . . , $S_m$ of subsets of $U$, and a number $k$, does there exist a collection of at most $k$ of these sets whose union is equal to all of $U$?
Vertex Cover $\le _{p}$ Set Cover

Satisfiability Problem (SAT)

Given a set $X$ of n Boolean variables $x_1,\dots,x_n$
A clause is simply a disjunction of distince terms $t_1\lor t_2 \lor \cdots\lor t_l (t_i\in\{x_1,x_2,\dots,x_n,\overline{x_1},\dots,\overline{x_n} \})$. We say the clause has length $l$ if it contains $l$ terms

A truth assignment for $X$ is an assignment of the value 0 or 1 to each $x_i$; in other words, it is a function $v: X\rarr \{0, 1\}$ An assignment satisfies a clause $C$ if it causes $C$ to evaluate to 1 under the rules of Boolean logic.
An assignment satisfies a collection of clauses $C_1,\dots, C_k$ if it causes all of the $C_i$ to evaluate to 1. In this case, we will say that $v$ is a satisfying assignment with respect to $C_1,\dots,C_k$; and that the set of clauses $C_1,\dots,C_k$ is satisfiable.

Problem Statement
Given a set of clauses $C_1,\dots,C_k$ over a set of variables $X=\{x_1,\dots,x_n\}$, does there exist a satisfying truth assignment?

3-SAT: all clauses contain exactly three terms

efficient certification:
to show efficient certification:

• Polynomial length certificate
• Polynomial time certifier the certifier is basically an algorithm that takes the certificate and decides whether or not it is a good solution.

NP(Non deterministic polynomial) is the set of all problems for which there exists an efficient certifier.

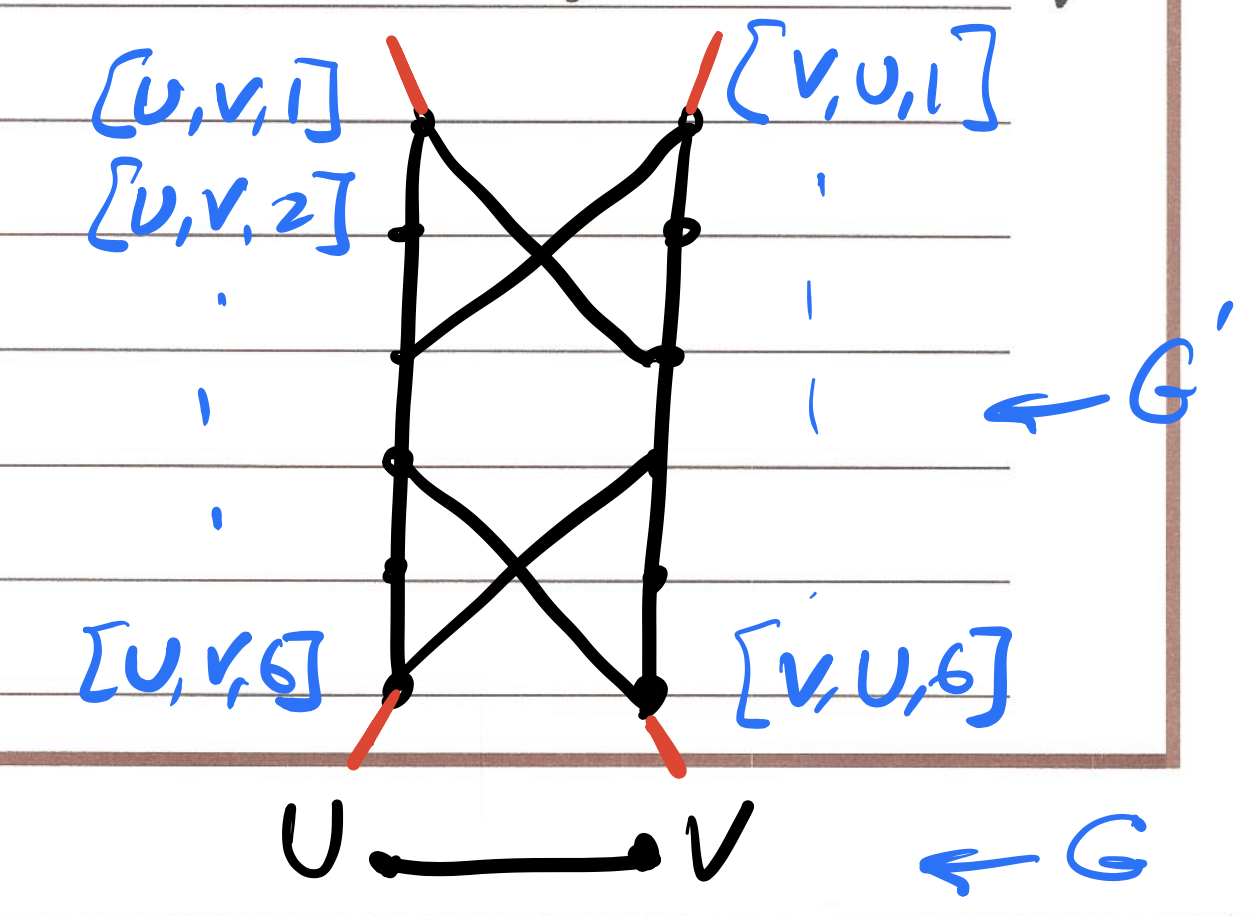
The Hamiltonian Cycle Problem

Given a directed graph $G=(V, E)$, we say that a cycle in G is Hamiltonian Cycle if it visits each vertex exactly once.
The Hamiltonian Cycle Problem is then simply the following: Given a directed graph G, does it contain a Hamiltonian cycle?
Show Hamiltonian Cycle Problem is NP-Complete:
Prove Vertex Cover is polynomial reducible to Hamiltonian Cycle Problem

The Traveling Salesman Problem

Order the cities into a tour $v_{i_1}, v_{i_2}, \dots ,v_{i_n}$, with $i_1=1$, so as to minimize the total distance $\sum_jd(v_{i_j}, v_{i_{j+1}}) + d(v_{i_n}, v_{i_1})$
Decision version of the Traveling Salesman Problem: Given a set of distances on n cities, and a bound D, is there a tour of length at most D? TSP is polynomial reducible to Hamiltonian Cycle Problem

Prove a problem is NP-Complete

• Prove X belongs to NP
• Choose a problem Y that is known to be NP-Complete
• Prove that Y$\leq_p$X